📉 When Math Becomes Performance Art: The AAAI 2023 Pearson Circus

[Sylvia]

“Sometimes, a proof doesn’t prove — it just performs.”

If you thought all math proofs in top AI conferences were solid as a rock, think again. Let me introduce you to an unforgettable gem from AAAI 2023: the paper Metric Multi-View Graph Clustering by Yuze Tan et al., which boldly attempts to re-prove the well-known fact that the Pearson correlation coefficient lies within the range [-1, 1]. The result? A demonstration that would make high school math teachers faint and TikTok comedians proud.

---

The Magical Disappearing Domain

For the uninitiated: the Pearson correlation coefficient between two vectors is mathematically guaranteed to lie in [-1, 1], thanks to the Cauchy-Schwarz inequality. It’s standard textbook stuff.

But our AAAI adventurers were not content with dusty math truths. No, they had a mission: to prove it anew. And their chosen method? Assume that one vector is a linear transformation of another, and compute:

Voilà! They have “proven” that the correlation is either +1 or -1. 🪄

What happened to all the intermediate values in (-1, 1)? Apparently, they took a break.

---

Wait... What?

This “proof” ends up asserting that Pearson correlation is always either -1 or 1 if there's a linear dependency, which is… not how range proofs work. It’s a bit like proving “all people are 6 feet tall” by only considering NBA players.

---

Of Dogs and Diagrams

To illustrate their “linearity-aware metric,” the authors even threw in a circle diagram showing dog breeds and angular distances.

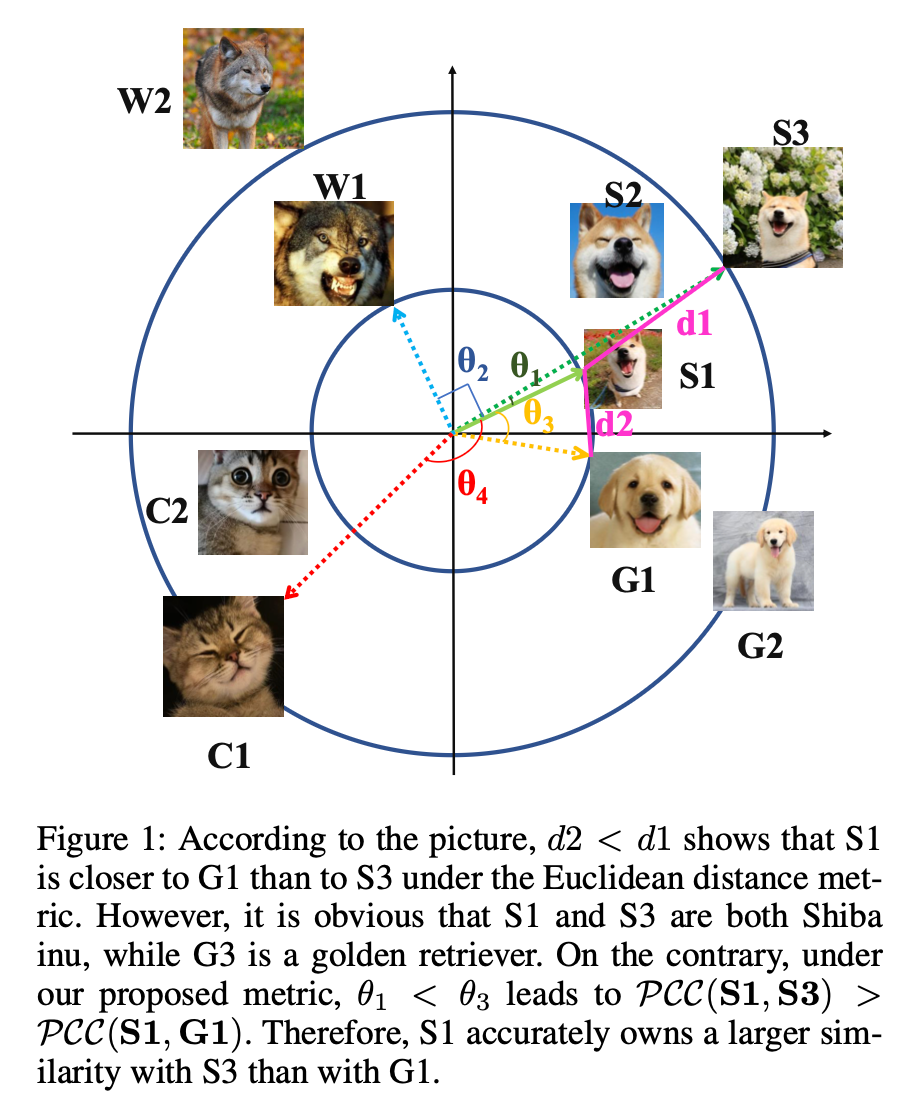
It’s cute — and makes for a nice graphic — but it doesn’t fix the fact that the underlying proof logic is fundamentally broken.

---

🧠 A Lesson in Math (or Lack Thereof)

This approach confuses a special case (collinear vectors) with a general property. To properly prove boundedness, you need to show it holds across all vector pairs, not just cherry-picked ones.

It's like proving "all fruits are apples" by only looking at apples.

---

How Did This Pass Peer Review?

Even more incredibly, this section made it into TKDE, a leading journal. That’s like publishing fanfiction in Nature.

Possible reasons:

• Reviewers focused only on clustering results.
• Theorem was seen as filler, not substance.
• Reviewer: “Looks mathy. ”

---

The Broader Problem with Peer Review

This paper highlights a systemic issue in AI peer review:

• Proofs are often unchecked.
• “Theorem + Corollary + Proof” is seen as a formality.
• Math becomes aesthetic, not analytic.

As one Zhihu commenter put it:

“导师说，要有 theorem，于是就有了。”
(“The advisor said the paper must have a theorem, so a theorem appeared.”)

---

🧩 Final Thoughts

To be fair, the paper still offers an actual clustering algorithm and decent empirical results. But the proof? It’s math theater. 🧵

Next time you see "Proof 1," brace yourself — you might be watching a circus act.

[Hu8kKo34]

Lol, it's funny ... I have seen authors make the theory unnecessarily overloaded

[Joanne]